
El Ensanche de Cerdà
Geometría de las manzanas del Ensanche
La geometría de las manzanas del Ensanche viene definida por una serie de parámetros muy bien elegidos, ya que la mayoría de ellos son enteros y fáciles de recordar. Podemos encontrarlos casi todos en esta imagen extraída del Centre de Cultura Contemporània de Barcelona; los que no aparecen explícitamente son fáciles de deducir mediante fórmulas muy simples.
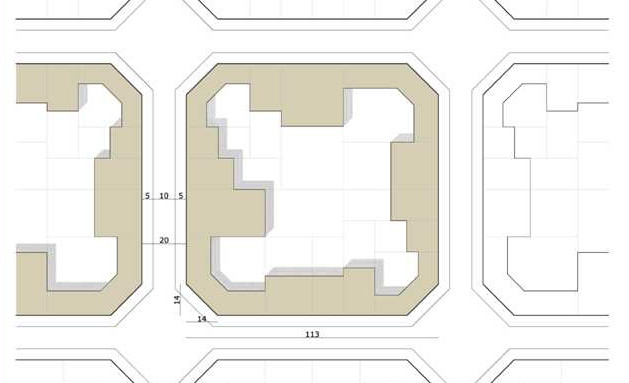
Veamos los parámetros más usuales:
- Las manzanas tienen una anchura de $133 = 113 + 20$ metros. Su superficie total es de $133\cdot 133 = 17689$ metros cuadrados.
- La anchura de la calle es de $20 = 5 + 10 + 5$ metros (acera + calzada + acera).
- Por tanto, la parte edificable tiene una anchura de $133-20 = 113$ metros.
- Los chaflanes miden $19.8$ metros.
- Los lados del triángulo rectángulo cuya hipotenusa es el chaflán miden los dos $\frac{19.8}{\sqrt{2}} = 14.000714... \sim 14$ metros (con un error $\lt 1$ milímetro).
- La parte central de la manzana mide $113 - 2\cdot 14 = 85$ metros.
- La superficie de un chaflán es de $\frac{{14}^2}{2} = 98$ metros cuadrados.
- La superficie edificable de una manzana es ${113}^2 - 4\cdot 98 = 12377$ metros cuadrados.
- La diagonal de una manzana mide $133\sqrt{2} = 188.090$ metros.
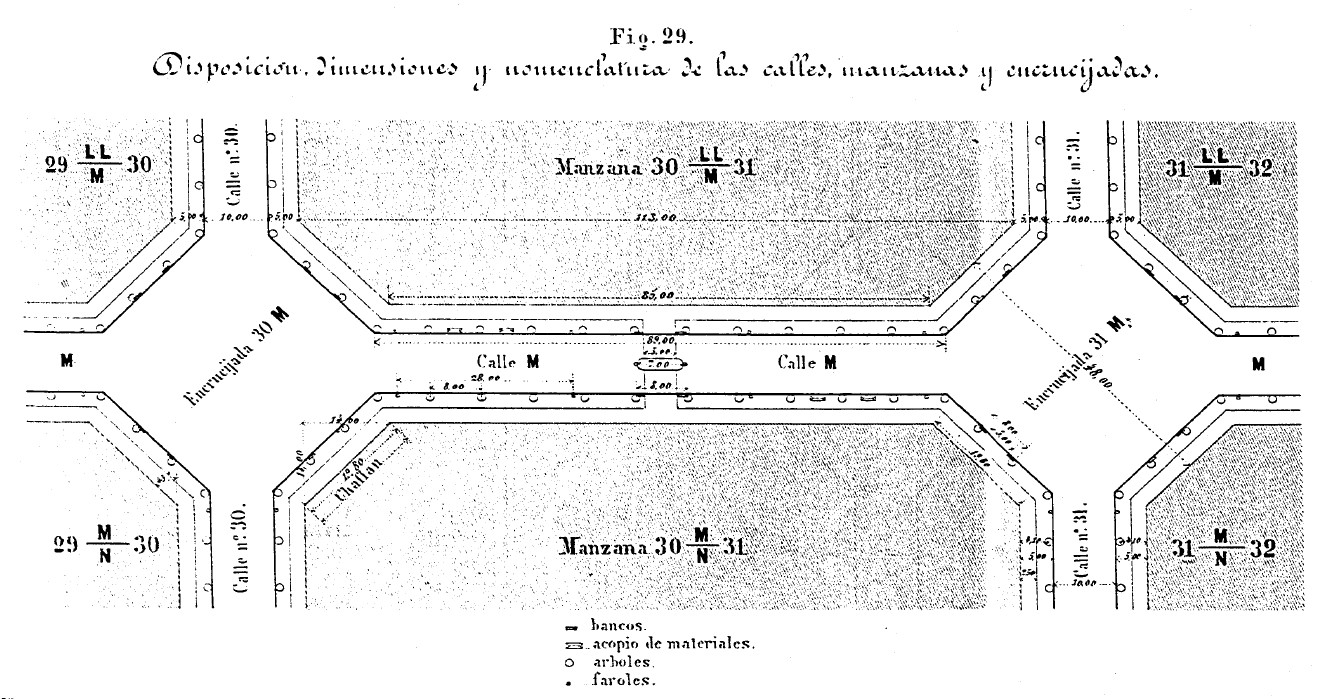
Como justifica Cerdà su elección del tamaño de las manzanas
La manera en la que Cerdà justifica la aparición del número 113, en su Teoría de la Construcción de las Ciudades, es más bien curiosa.
[...] Se tendrá para las manzanas [...] Abiertas [...] con chaflanes
\[ x = \frac{pv-2bd}{d}\pm \sqrt{\frac{pv}{d^2f}(pvf-4bdf-4b^2d)} \]Aplicando ahora a estas fórmulas los siguientes valores constantes: 2b = 20[,] f = 20[,] d = 20[,] p = 40[,] y suponiendo ademas que los valores de V sean 71[,] 57[,] 43[,] 29[.] Obtendremos los dos siguientes estados: [...]
Ildefonso Cerdà, Teoría de la Construcción de las Ciudades aplicada al Proyecto de Reforma y Ensanche de Barcelona (1859), en Teoria de la Construcción de las Ciudades. Cerdà y Barcalona, volumen 1. Madrid: Ministerio para las Administraciones Públicas y Ajuntament de Barcelona, 1991, p. 413 [1497].
Para $v = 43$, se obtiene $x=113.286$, redondeado al milímetro más cercano. Con calles de $20$ metros, las manzanas medirían, entonces, $133.286$ metros, de modo que a una sucesión de tres manzanas le faltarían sólo $141$ milímetros para medir exactamente $400$ metros.
Cerdá, sin embargo, parece no querer hacer nada con los decimales del resultado, pues continúa:
Entre los diversos valores que resultan de la construcción de las fórmulas, ¿cual es el que deberemos adoptar? En nuestro concepto es el que nos dá para la manzana $113$ metros de lado.
Ibid., p. 420 [1489].
En la práctica, las manzanas no miden exactamente $133$ metros, sino que experimentan pequeñas variaciones, en general por exceso. Suele ser una buena regla contar que tres manzanas son aproximadamente $400$ metros; eso nos permite hacer cálculos rápidos bastante útiles.
Las vías más anchas
Cuando una vía es más ancha de los veinte metros estándar, la parte extra de la anchura se ve compensada por una disminución del tamaño de las manzanas que bordean la vía. Por ejemplo, la calle de Urgell [20] tiene treinta metros de ancho, es decir $30-20 = 10$ metros más de lo estándar, de modo que cada una de las manzanas adyacentes deberá repartirse la mitad de esos diez metros, es decir, cinco, y tendrá $113-5=108$ metros de ancho, en vez de los $113$ estándar.
Esta regla se cumple para todas las calles, en el proyecto de Cerdà, excepto para la Gran Vía [N]. En este caso especial, las manzanas que bordean la calle son perfectamente normales, no les falta nada. De este modo, y hablando con propiedad, el Ensanche de Cerdà no forma una cuadrícula, sino dos, una situada por encima de la Gran Vía [N] y otra por debajo.
Por la misma razón, cuando se calcule alguna distancia que involucre cruzar la Gran Vía [N], habria que añadir manualmente los treinta metros extras, porque las fórmulas clásicas (tres calles son $400$ metros) dejarán de funcionar.
Algunos cálculos de ejemplo
Los siguientes cálculos, que se ofrecen a modo de ejemplo, son todos aproximados. Las diferencias con las mediciones efectivas pueden achacarse, en muchos casos, a imperfecciones de las alineaciones.
- Anchura de la ciudad vieja. Los dos lados de la ciudad vieja están delimitados por la calle de Urgell/Sant Pau [20] y el paseo de Sant Joan/Lluis Companys [35]. La distancia es de $35-20 = 15$ manzanas; pero $15 = 5\cdot 3$, y $3$ manzanas son $400$ metros; por lo tanto, la ciudad vieja ocupa exactamente $5 \cdot 400 = 2000$ metros $= 2$ kilómetros.
- Altura del Ensanche. De Olesa [C] a Villena [Z] hay exactamente $23$ manzanas, es decir, $23 = 7\cdot 3 + 2$ manzanas $= 7\cdot 400$ metros $+ 2*133= 3.066$ kilómetros, a lo que hay que sumarle treinta metros, porque atravesamos la Gran Vía [N], es decir, $3.096$ kilómetros.
- Avenida de Gaudí. La Avenida de Gaudí atraviesa cuatro manzanas, y por tanto mide $4\cdot 188 = 752$ metros.
- Longitud de Sancho d'Àvila [R]. Empieza en Lepanto [41] y termina en la rambla del Poblenou [50], y por tanto son $9$ manzanas $= 3\cdot 3$ manzanas $=3 \cdot 400$ metros $=1.2$ kilómetros.
Comentarios a josep.maria.blasco@epbcn.com. Una web hecha en ooRexx y RexxHttp.